Дисконтированный срок окупаемости инвестиционного проекта
Дисконтированный срок окупаемости инвестиционного проекта — период времени за который чистый дисконтированный доход нарастающим итогом станет равным нулю. Часто используется обозначение DPBP или DPP от англ. Discounted Payback Period.
Определение из известного учебника Л.Я. Лукасевич «Финансовый менеджмент»:
«В математическом отношении дисконтированный срок окупаемости представляет собой период времени, когда NPV проекта становится равной 0»
NPV проекта (Net Present Value, чистая приведенная стоимость) — это общепринятое обозначение для чистого дисконтированного дохода нарастающим итогом.
Содержание
Смысл показателя «Дисконтированный срок окупаемости»Срок окупаемости инвестиционного проекта
Простая формула расчета срока окупаемости
Срок окупаемости в реальных инвестиционных проектах
Математическая формулировка срока окупаемости инвестиционного проекта
Формула более точного расчета срока окупаемости
Дисконтированный срок окупаемости инвестиционного проекта
Выводы
Смысл показателя «Дисконтированный срок окупаемости»
Термин дисконтированный срок окупаемости инвестиционного проекта означает, что рассчитывается срок окупаемости проекта с учетом временной стоимости денег. То есть, с учетом того, что реальная стоимость суммы денег имеющейся в настоящий момент, выше стоимости равной ей суммы, которая появится в будущем. Стоимость будущих денежных потоков, приведенная к стоимости на текущий момент называется дисконтированной.
Рассмотрим сначала простой срок окупаемости, а затем дисконтированный срок окупаемости.
Срок окупаемости инвестиционного проекта
Срок окупаемости инвестиционного проекта — период времени за который чистый доход (ЧД), то есть, доходы минус расходы, нарастающим итогом станет равным нулю. Часто используется обозначение PBP или PP от английского Payback Period.
На первых этапах выполнения инвестиционного проекта затраты превосходят текущие доходы. Поэтому требуется вложение средств, которые будут источником развития проекта до тех пор, пока он не начнет приносить доход в размере покрывающем текущие затраты. Эти вложения называются инвестициями.
До наступления срока окупаемости ЧД нарастающим итогом был отрицательным, а после этого он станет положительным. То есть, с этого момента инвестор, окупив свои вложения, начинает получать прибыль, ради которой был начат инвестиционный проект.
Обратите внимание, именно чистый доход, т.е. доход минус расход.
Простая формула расчета срока окупаемости
Можно записать формулу расчета срока окупаемости, если сделать два предположения:
- Все инвестиции делаются в начале одномоментно или в течение небольшого промежутка времени.
- Доходы и расходы постоянны во времени или можно взять некоторые средние значения. Иными словами, ЧД постоянный.
Тогда формула расчета имеет вид:
Срок окупаемости = (Сумма инвестиций) / (ЧД за период) (*)
В качестве периода обычно берут месяц, квартал или год. Соответственно, величина срока окупаемости будет измеряться в месяцах, кварталах или годах.
Срок окупаемости в реальных инвестиционных проектах
В реальных инвестиционных проектах ЧД не является постоянным и сделать расчет срока окупаемости с помощью простого деления, как в формуле (*) невозможно.
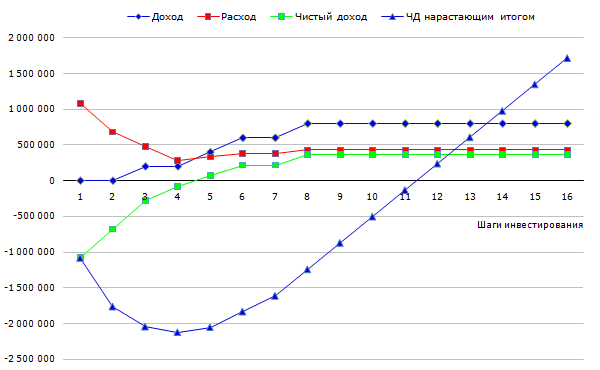
Обычно, график денежных потоков выглядит примерно так:
На приведенном графике в начале инвестиционного проекта доход равен нулю, потом доход появляется и растет по мере отладки производственных процессов и маркетинга. Потом бизнес выходит на проектную мощность и доход стабилизируется.
Расходы в начале инвестиционного проекта максимальны, потом расходы уменьшаются. Когда бизнес выходит на проектную мощность расходы стабилизируется.
Чистый доход в начале проекта отрицательный, далее он растет и становится положительным. Когда бизнес выходит на проектную мощность ЧД стабилизируется.
Математическая формулировка срока окупаемости инвестиционного проекта
Обычно, время реализации инвестиционного проекта разбивается на шаги инвестиционного проекта — периоды (месяц, квартал, год) по итогам которых осуществляется промежуточное подведение итогов.
Тогда ЧД нарастающим итогом за k шагов можно записать следующим образом.
CFk = (CF1+ - CF1-)+ (CF2+ - CF2-)+…+ (CFk+ - CFk-)
| CFk | ЧД нарастающим итогом за k шагов. Иногда используют обозначение NCF — Net Cash Flow, чистый денежный поток | |
| CFi+ | сумма доходов (положительный денежный поток) на i-м шаге | |
| CFi- | сумма расходов (отрицательный денежный поток) на i-м шаге | |
| i | = 1…k |
Если срок окупаемости составляет n шагов инвестиционного проекта, будет выполняться равенство
CFn = (CF1+ - CF1-)+ (CF2+ - CF2-)+…+ (CFn+ - CFn-) = 0 (**)
На всякий случай уточню, что выражение (**) не формула расчета срока окупаемости, а математическая формулировка определения из первого параграфа. Формулы по которой в общем случае можно рассчитать срок окупаемости не существует.
На самом деле такая формула не очень-то и нужна. Если сделаны расчеты для определения стандартных показателей инвестиционного проекта, срок окупаемости определяется очень просто.
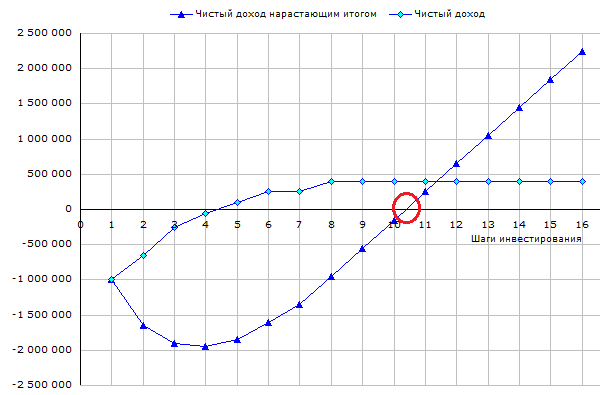
Рассмотрим таблицу и график денежных потоков некоторого инвестиционного проекта.
В приведенной выше таблице шаг 1 квартал (3 месяца). Срок окупаемости приблизительно 10.5 кварталов, это примерно два с половиной года.
Обычно срок окупаемости достигается не за целое число шагов, а имеет место следующая ситуация: на шаге n ЧД нарастающим итогом меньше 0, а на следующем (n+1)-ом больше нуля.
CFn < 0
CFn+1 > 0
В первом приближении можно считать, что срок окупаемости равен n+1/2 (n с половиной) шагов. Обычно такой точности бывает достаточно, тем более что при осуществлении инвестиционного проекта все равно будут отклонения от расчетных показателей.
Формула более точного расчета срока окупаемости
Если требуется точнее определить срок окупаемости, можно поступить следующим образом. Предположим, что на каждом шаге инвестиционного проекта ЧД нарастающим итогом растет линейно, тогда можно составить и решить пропорцию:
Ш-/Ш+ = CFna /CFn+1
| Ш- | часть шага, на которой ЧД нарастающим итогом меньше 0, | |
| Ш+ | часть шага, на которой ЧД нарастающим итогом больше 0, | |
| CFna | = |CFn| — абсолютная величина. |
Учитывая что
Ш+ + Ш- = 1
Ш+ = 1 - Ш-
можно записать
Ш-/(1-Ш-) = CFna /CFn+1
Решая относительно Ш-, получаем
Ш-= CFna/( CFna + CFn+1)
Таким образом, срок окупаемости равен n целых шагов и плюс
CFna/( CFna + CFn+1) часть шага.
PBP = n + CFna/(CFna + CFn+1)
Целое число шагов определяем по таблице чистого дохода, а дробную часть вычисляем. Подробнее с примерами расчетасрок окупаемости инвестиционного проекта.
Дисконтированный срок окупаемости инвестиционного проекта
Обычно, реализация инвестиционного проекта занимает продолжительное время, поэтому проявляется фактор зависимости стоимости денег от времени. То есть сумма денег, имеющаяся сейчас, имеет большую ценность, чем такая же сумма, которая будет получена в будущем. Это обусловлено несколькими причинами, например, имеющаяся сумма может принести прибыль, будучи вложена в какой-нибудь бизнес или положена на депозит в банке. Учет этого факта выполняется путем дисконтирования денежных потоков.
Операция вычисления дисконтированной стоимости обратна операции начисления сложных процентов. Процентная ставка, используемая при этих расчетах, называется ставкой дисконтирования.
Пусть, имеется поток платежей через равные промежутки времени:
CF = CF0 + CF1 + CF2 + … + CFK
В нашем случае денежные потоки это ЧД на шагах инвестиционного проекта. Применяя к каждому платежу операцию дисконтирования, получим формулу:
DCF = CF0 + CF1/(1+D) + CF2/(1+D)2 + ... + CFK/(1+D)K
DCF —дисконтированный денежный поток
D —ставка дисконтирования
Или, можно записать как:
DCF = DCF0 + DCF1 + DCF2 + … + DCFK,
где:
DCFn = CFn/(1 + D)n
Чем больше n, тем дальше в будущее отстоит от текущего момента (момента когда мы рассчитываем доходность инвестиционного проекта) дата очередного денежного потока. И тем меньше стоимость каждой денежной единицы, приведенной к текущей стоимости (дисконтированной). Математически это выражается в росте выражения, стоящего в знаменателе: (1 + D)n.
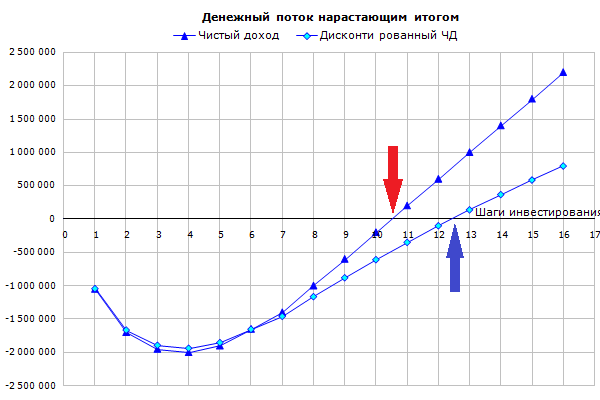
Вот, как это выглядит на графике.
Видим, что с ростом n линия дисконтированного чистого дохода все больше отстает от линии чистого дохода.
На графике видно, что срок окупаемости (показан красной стрелкой) меньше дисконтированного срока окупаемости (показан синей стрелкой).
Все соображения, математические выкладки и формулы для расчета срока окупаемости применимы и к дисконтированному сроку окупаемости. Для дисконтированного срока окупаемости можно записать формулу, аналогичную простому сроку дисконтирования:
DPBP = n + DCFna/(DCFna + DCFn+1)
Целое число шагов определяем по графику или по таблице дисконтированного чистого дохода, а дробную часть вычисляем по формуле.
Выводы
- Срок окупаемости инвестиционного проекта — период времени, за который чистый доход нарастающим итогом станет равным нулю.
- Дисконтированный срок окупаемости — это период времени, за который чистый дисконтированный доход нарастающим итогом станет равным нулю.
- Срок окупаемости меньше дисконтированного срока окупаемости.
- Формулы расчета срока окупаемости и дисконтированного срока окупаемости в общем случае не существует.
- С достаточной точностью срок окупаемости (в том числе дисконтированный) можно определить по таблице денежных потоков на шагах инвестирования. Если вы делаете расчеты инвестиционного проекта в Excel, логично сделать и расчет срока окупаемости по алгоритму описанному выше.
По теме статьи и другие полезные ссылки
Список таблиц финансовых расчетовКарта сайта — Подробное оглавление сайта.
Гостевая книга — отзывы и вопросы