Дисконтирование денежных потоков
Формула расчета и примеры
Онлайн калькулятор
Дисконтирование денежных потоков — приведение стоимости потоков платежей, выполненных в разные моменты времени, к стоимости на текущий момент времени.
Дисконтирование отражает тот экономический факт, что сумма денег, которой мы располагаем в настоящий момент, имеет большую реальную стоимость, чем равная ей сумма, которая появится в будущем. Это обусловлено несколькими причинами, например:
- Имеющаяся сумма может принести прибыль, например, будучи положена на депозит в банке.
- Покупательная способность имеющейся суммы будет уменьшаться из-за инфляции.
- Всегда есть риск неполучения предполагаемой суммы.
Это делается, например, при оценке эффективности инвестиционных проектов или в методе дисконтирования денежных потоков в рамках доходного подхода оценки стоимости бизнеса.
Смысл операции дисконтирования
Поясним смысл операции дисконтирования денежных потоков на следующем примере.
Пример
Пусть мы имеем 100 руб. и кладем их на депозит под 5% годовых с ежегодным начислением процентов и зачислением их во вклад. Тогда через год у нас будет 105 рублей.
S1 = 100 + 100 × 0.05 = (1+0.05) × 100 = 105
Через два года у нас будет 110.25 рублей.
S2 = (1+0.05)×(1+0.05) × 100 = (1+0.05)2 × 100 = 110.25
Через три года у нас будет 115.7625 рублей.
S3 = (1+0.05)3 × 100 = 115.7625
Через n лет у нас будет
Sn = (1+0.05)n × 100
В общем виде формула выглядит так
Sn = (1+P)n S0, где
Sn — сумма через n периодов начисления процентов
P — процентная ставка за период
S0 — начальная сумма.
Это формула расчета сложных процентов.
Таким образом, если мы можем положить деньги на депозит с условиями описанными выше, то 100 руб., которые мы получим сейчас, с экономической точки зрения равноценны 105 руб. которые мы получим через год, равноценны 110.25 руб. полученным через два года, равноценны 115.7625 руб. полученным через три года и так далее.
В общем виде: сумма S0, полученная сейчас, равноценна сумме (1+P)n S0, полученной через n лет.
Формула дисконтирования
Часто возникает обратная задача: предполагается, что через n лет будет получена сумма Sn, надо найти равноценную ей сумму на текущий момент. Это типичная задача при разработке бизнес-планов, расчете окупаемости инвестиций, оценке стоимости бизнеса по величине ожидаемых доходов (доходный подход к оценке стоимости бизнеса). Иными словами, известна сумма Sn, надо определить S0. В этом случае путем простых преобразований получаем формулу расчета:
S0 = Sn/(1+P)n — Формула дисконтирования
Эта операция называется дисконтированием, она является обратной к вычислению сложных процентов. Часто используется термин «приведение к текущей стоимости». Процентная ставка в этом случае называется ставкой дисконтирования.
Денежные потоки
При расчете инвестиционных проектов и при оценке бизнеса имеют дело с многократными поступлениями и оттоками денежных средств. Обычно их группируют по некоторым периодам времени (год, квартал, месяц) и суммируют.
Получившиеся значения называются денежными потоками. Денежные потоки могут быть положительными (сумма поступлений за период превышает сумму оттоков) и отрицательными (сумма оттоков за период превышает сумму поступлений).
Коэффициент дисконтирования
Дисконтирование денежного потока за n-й период выполняется путем умножения потока на коэффициент дисконтирования Kn:
Kn= 1/(1+D)n, где
n — Номер периода (шага) дисконтирования
Kn — Коэффициент дисконтирования на шаге n
D — Ставка дисконтирования.
Ставка дисконтирования отражает скорость изменения стоимости денег со временем, чем больше ставка дисконтирования, тем больше скорость.
Коэффициент Kn уменьшается с ростом n, это отражает тот факт, что чем дальше в будущее отстоит от нас ожидаемый денежный поток, тем меньше его стоимость приведенная к текущему значению.
См. также:
Формула дисконтирования денежных потоков
Если имеется поток платежей через равные промежутки времени:
CF = CF0 + CF1 + CF2 + … + CFN,
то применяя к каждому платежу операцию дисконтирования, получим формулу:
CFd = CF0 + CF1/(1+D) + CF2/(1+D)2 + … + CFN/(1+D)N
CFd — дисконтированный денежный поток,
или в более компактном виде:
CFd = ∑0N CFn /(1+D)n
Первый денежный поток CF0 не дисконтируется, если это платежи текущего периода или продолжительность периодов на которых вычисляются потоки мала, то есть нет смысла дисконтировать.
Если имеет смысл делать дисконтирование первого денежного потока, формула дисконтирования примет вид:
CFd = ∑1N CFn /(1+D)n
Один из примеров дисконтирования денежных потоков — чистый дисконтированный доход (NPV), в котором денежными потоками выступают итоги (приход - расход) на каждом шаге инвестиционного проекта.
Онлайн калькулятор
Дисконтирование денежных потоков
Дисконтированный поток =
Примеры расчета дисконтированных денежных потоков
Показанные ниже расчеты и графики выполнены в таблице Расчет инвестиционных проектов
Пример 1. Оценка бизнеса
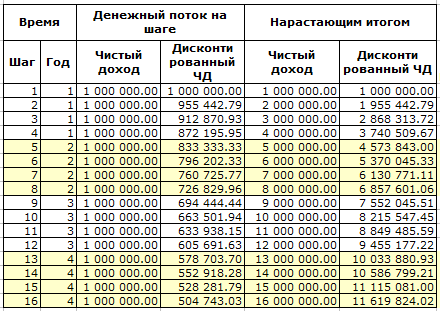
Ниже показаны денежные потоки (чистый доход = доходы минус расходы) некоторого оцениваемого бизнеса. Шаг дисконтирования (период времени на котором суммируются платежи и поступления) 3 месяца. Ставка дисконтирования 20% годовых.
Обратите внимание, что суммарный чистый доход равен 16 000 000, а суммарный дисконтированный чистый доход равен 11 619 824.
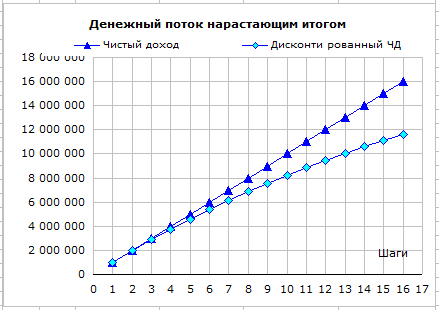
Ниже показаны графики нарастающим итогом денежных потоков и дисконтированных потоков оцениваемого бизнеса.
Видно, что график дисконтированного чистого дохода с каждым шагом все больше отстает от графика чистого дохода. Как уже было отмечено, это отражает тот факт, что чем дальше в будущее отстоит от нас ожидаемый денежный поток, тем меньше его стоимость приведенная к текущему значению.
Пример 2. Расчет инвестиционного проекта
Более сложный случай — инвестиционный проект. Характерная черта инвестиционных проектов — отрицательные денежные потоки (убытки) на первых этапах. Далее доход, приносимый проектом, постепенно растет и перекрывает первоначальные убытки.
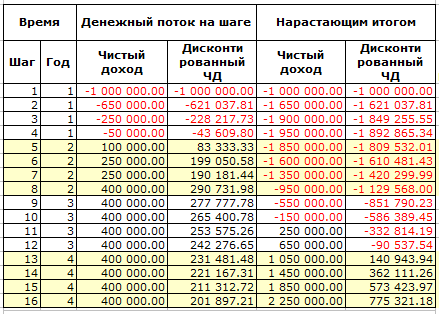
Ниже показаны денежные потоки (чистый доход) некоторого инвестиционного проекта. Шаг инвестиционного проекта (период времени на котором суммируются платежи и поступления) 3 месяца. Ставка дисконтирования 20% годовых.
Обратите внимание, что суммарный чистый доход равен 2 250 000, а суммарный дисконтированный чистый доход равен 775 312.
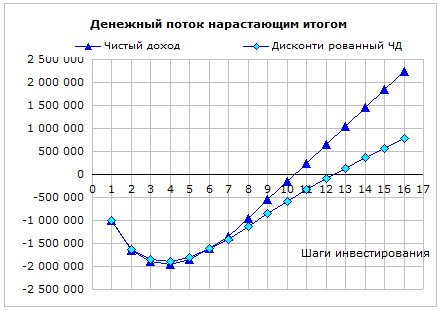
Ниже показаны графики нарастающим итогом денежных потоков и дисконтированных денежных потоков этого инвестиционного проекта.
Видно, что график дисконтированного чистого дохода с каждым шагом все больше отстает от графика чистого дохода.
Точка, в которой график пересекает ось времени, определяет период окупаемости. На графике видно, что простой период окупаемости (PBP — payback period) составляет примерно 10 и 1/3 шага или 31 месяц, а период окупаемости с учетом дисконтирования (DPBP — discount payback period) составляет примерно 12 и 1/2 шага или 37.5 месяцев. Подробнее см. расчет срока окупаемости инвестиционного проекта.